![[PukiWiki]](image/pukiwiki.png "[PukiWiki]")
縦、横に配置すると光は通ってこないのはよく知られている。間に斜めの直線偏光となる偏光板を配置するとどうなるか？またどう解釈する？量子論的解釈では斜めの後は斜め。振幅の２乗が透過個数になるはず。
原子物理では縮退しているエネルギー準位の関係で動径方向の量子数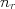
を使って主量子数
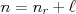としていることに注意する。素粒子・原子核物理では動径方向の量子数をそのまま使うのが普通。
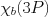がその例。
最近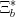
をCMSが見つけたらしいが、ATLASも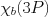を見つけたというのが検索にかかった。
まずは物理学実験で行った、核磁気共鳴を思い出す。ある周波数で電波の吸収が起こる。
吸収は陽子核スピンの才差運動によって起きている。
物理量は状態を表す波動関数と演算子の期待値となる。波動関数は位置と時間依存性のほかのスピンやアイソスピンなど内部状態も含むので話がややこしくなる。内部状態関連の物理量の計算は位置の依存性を持つ計算方法から類推する。
まずは物理量演算子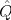
から期待値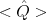
を計算したものが物理量となるという表現方法に慣れること。
物理量演算子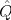が実数になってくれるものをエルミート演算子とよぶ。また、ある状態の期待値をとると複素数になってしまう演算子
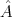に対し、同じ状態の期待値がその複素共役になるものをエルミート共役演算子
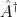と呼ぶ。調和振動子の生成、消滅演算子や角運動量の昇、降演算子がそれにあたる。
角運動量が２の緯度方向の波動関数をプロットしてみる。磁気量子数の絶対値が2,1,0の順番。2のときx,y平面に多く存在するということを示す。また磁気状態が5個あることに注意する。
plot [0:3.141592] sqrt(15./32.)*sin(x)*sin(x), sqrt(15./8.)*sin(x)*cos(x), sqrt(5./16.)*(3*cos(x)*cos(x)-1)
水素原子ではエネルギーが-13.6/n^2で固有状態となる。ここではルンゲ・クッタ法で境界条件を満たす固有値を探すプログラムとなる。普通はFortranでやるべきところをcでやるとコピーが好きなcのおかげで、メモリーの場所のやりとりに記述を置き換えるはめになる。
主量子数が増えると角運動量子数をそれより小さくとる。
これらのコードをダウンロードして、コードを見てみる。基本的には動径方向の波動関数をgnuplotで描画するように数値を表示するようになっている。
0.1nmでエネルギーが10eVの電子波の様子。横軸は位置で単位はnm。
その電子波の確率分布の移動の様子のgnuplotを使ったアニメーション。
波と粒子の性質を妥協しようとすると両方のガウス分布の標準偏差の積を最小値が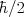
となることがわかる。波と粒子の描像を共存させようとすると、散乱断面積などで見られるように、古典物理ではインパクトパラメータで散乱角が決定されるのに対し、量子力学では平面波がそれぞれの方向に散乱される確率を決めるだけになる。決定論から確率的記述に移行する。
数値としては、betaが0.006256で、広がりの速度の光速度比が0.001927なので、それぞれ30をかけた数値がフレームごとに増えていくことになっている。しいて解釈すると0.1femto秒ごとに描画することを30回繰り返すループとなっている。光電効果ぐらいのエネルギーを持って飛び出した電子の原子ぐらい大きさの波束が3femto秒後には何十倍も広がってしまうということ。
E/V0をxとすると、xが１より小さい場合がトンネル効果の場合。プログラムの中にあるV0Gap2mは障壁の大きさを示す。針に電圧をかけてトンネル効果を示すにはギャップが原子の大きさである必要が分かる。また針の先端も原子の大きさが必要。トンネル顕微鏡を動作させるのが大変であることが分かる。ナノテクは大変な技術。
g77 -o transmission transmission.f ./transmission > t.dat gnuplot plot 't.dat' , 't.dat' using 1:3 , 't.dat' using 1:4
教科書（岩波基礎物理シリーズ）には障壁の比較的大きい場合の近似式がある。これもプロットしてみよう。
振動に決まった（とびとびの）振幅しかないような理論を信じると比熱もその影響を受ける。固体の振動子の基本振動のエネルギーに対する周りの温度の比をxとして、その温度の時の比熱のデュロンプティの3Rに対する比の式は以下のプロットコマンドになる。
plot [0:5] 1/(x*x)*exp(1/x)/(exp(1/x)-1)**2
原子の中を電子が運動する速度
を使っていろんな量を計算するのが前期量子論。興味深い物理量が計算できる。遠心力のつり合いと角運動量の量子化の式から、量子化されたエネルギーの値やボーア半径が求まる。
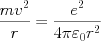・・・(1)
・・・(2)あまりありがたくない速度をこれを使って消すとボーア半径の式になる。量子化されたエネルギーはポテンシャルエネルギーの半分であることに注意すると、それを表す式が求まる。微細構造定数と自然単位（原子物理学用）を使ってこれを計算すると基底状態が13.6eVとなる。
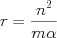・・・(3)
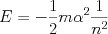・・・(4)この仮想的な速度を使うと、ゼーマンエネルギーの式が求まる。原子の中の電流を電荷と周回回数の積とし、周回する面積の積が磁気能率となり、磁束密度をかけたものがゼーマンエネルギーとなる。
この関係を電子に適用すると、スピンが1/2なので、角運動量は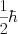
のはずだが、ゼーマンエネルギーは2倍になる。これを説明するには、電子スピンの起源を相対性論的な波動方程式に求めると良いことがディラックによって示された。角運動量が反転するので、その2倍が共鳴エネルギーとなる。
これらを3回生前期の物理学実験では核磁気共鳴装置を使って調べることができる。ただし、共鳴周波数の推測には他の重粒子との対称性を考えて、クォークの波動関数が使われる。
原子の世界にたどり着くには、黒体輻射、樹脂の垂直分布、素電荷の他にもう一つ道がある。拡散による、位置の分散は２かける拡散係数かける時間となる。
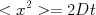・・・(5)拡散係数はボルツマン定数かける温度をlinear drag coefficientで割ったもの。
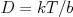・・・(6)ストークスの法則は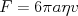
であるから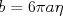
となる。樹脂粒子の大きさがわかっていれば、拡散の様子からボルツマン定数が求まる。「X線からクォークまで」（セグレ著）に簡単な導き方が書いてある。
これらを半導体のキャリアー分布に適用して、ｐｎ接合のビルトイン電圧の計算に用いられる。半導体のlinear drag coefficientは電場による力が抵抗と関係づけられて、比抵抗とキャリアー密度と素電荷の2乗の積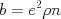
となる。
http://www.phys.u-ryukyu.ac.jp/~maeno/JavaQM/index.html
http://ja.wikipedia.org/wiki/%E3%83%97%E3%83%A9%E3%83%B3%E3%82%AF%E5%88%86%E5%B8%83
1900年の物理学会の報告に基づいて1901年の論文誌に報告された論文で、ボルツマン定数とプランク定数をのせている。計算方法は、自らの輻射公式から計算したステファンボルツマンの法則による放熱の温度依存の測定、ウィーンの変位則からの数値は共に違った形でこの二つの定数を含んでいるため計算ができる。学生実験に良いテーマかも。ニクロム線の温度から推定する。
自由度の計算の時に空洞の中の定在波の数で数えるのと、周期的境界条件で数えるのとは同じになる。教科書によっては、自然数の定在波で数える場合と、周期的境界条件の整数で数えるのとがあるので注意しよう。直感的には定在波のほうが今の場合には自然だが、一般化しようとすると整数のほうが右向き左向きの波を個別に扱うので拡張性があるみたい。
ボルツマン定数はアボガドロ数を決めてしまう数値のため、この時点で原子の存在について基本的な数値が得られていたことになる。ペランが樹脂の粒の垂直分布からボルツマン定数を求めたのはこの5年後。
量子論は真空の比熱の研究から生まれた。身近に比熱が出てくるのは圧縮発火実験。ポアソン比が空気の等圧比熱/定積比熱であることから、圧縮比に対してどのような温度上昇がおこるかを実験で知る。圧縮比に対する絶対温度はgnuplotで予想する。
gnuplot plot [1:20] (273+20)*x**0.4
偶関数の解はポテンシャルの深さにより、以下のグラフで、運動量をパラメータとしてもとまる。
set grid plot [0:4][0:4] sqrt(1-x**2),sqrt(4-x**2),sqrt(16-x**2),x*tan(x)
set samples 300 plot [0:0.3] [0:110] plot sin(5*x)/x,sin(10*x)/x,sin(20*x)/x
回折現象もよく似たスパイク状の関数になる。
plot [0.0.3] [0:110] sin(9.93*sin(x))**2*sin(496*sin(x))**2/(sin(49.6*sin(x))**2*sin(x)**2)/100. linewidth 2
http://natsci.kyokyo-u.ac.jp/~takasima/mydoc/butsu2/butsu2.html
myRotSpinSave.C