![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
ニュートンが見いだした運動の法則を単振動に適用して、計算機で数値解を求めてみましょう。gfortranかg77を使ってデータファイルを作ります。その後、gnuplotで結果を見てみます。筑波大学の原子核理論のHPにあったプログラムです。
gfortran -o springEuler springEuler.f ./springEuler gnuplot plot 'Newton_Euler.dat', 'Newton_Euler.dat' using 1:3
Runge Kutta法を用いると精度が上がります。同じようにプロットを作成しましょう。
力学的世界観とは自分を地球の外に持っていく視点を持つこと。例えば「地球はでっかいジャイロスコープ」なんてことがピンとくる人になること。おもちゃの「地球ごま」などもそのたぐい。おもちゃを地球に例えるわけです。そしてその原理を角運動量の保存という物理法則に求めることができればあなたも立派な物理愛好家。
この運動方程式は一般化座標を使って解くことができる。変分法を使うなどして、棒の長さがそれぞれ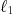 と
と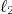 で質量が
で質量が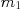 と
と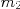 、鉛直となす角が
、鉛直となす角が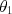 と
と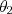 の振り子の運動エネルギー
の振り子の運動エネルギー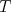 を
を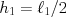 、
、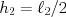 として求めると
として求めると
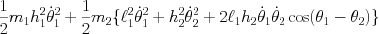 ・・・(1)
・・・(1)となる。位置エネルギー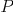 は幾何学的に求まる。不思議なことに最小作用の原理を適用するのは
は幾何学的に求まる。不思議なことに最小作用の原理を適用するのは でなく
でなく である。これから方程式を作って、ルンゲクッタ法で時間発展を計算する。
である。これから方程式を作って、ルンゲクッタ法で時間発展を計算する。
http://www-eng.kek.jp/giken/procedng/paper/met005.pdf
ベアリングはミニ四駆の四隅につけるガードベアリングをヨドバシで買った。アルミの棒に穴をあけて取り付ければOKなはず。M2.6のタップセットをアマゾンで注文した。
二重振り子のラグランジアンは変分の考え方で、運動エネルギー引くポテンシャルエネルギーを計算して作る。作った後の時間発展は、ルンゲクッタ法の良い利用例となる。やってみよう。
物理天秤というものがある。水の中の重さの向きを変える実験が行える。